Ninguém sabe ao certo quem descobriu o pi

Tente medir um círculo. O diâmetro e o raio são fáceis, são apenas linhas retas que você pode medir com uma régua. Mas para obter a circunferência, você precisaria de uma fita métrica ou um pedaço de barbante, a menos que houvesse uma maneira melhor. Agora, é óbvio que a circunferência de um círculo diminuiria ou aumentaria junto com seu diâmetro, mas a relação vai além disso. Na verdade, a razão entre os dois, a circunferência dividida pelo diâmetro, sempre será o mesmo número, não importa quão grande ou pequeno o círculo fique.

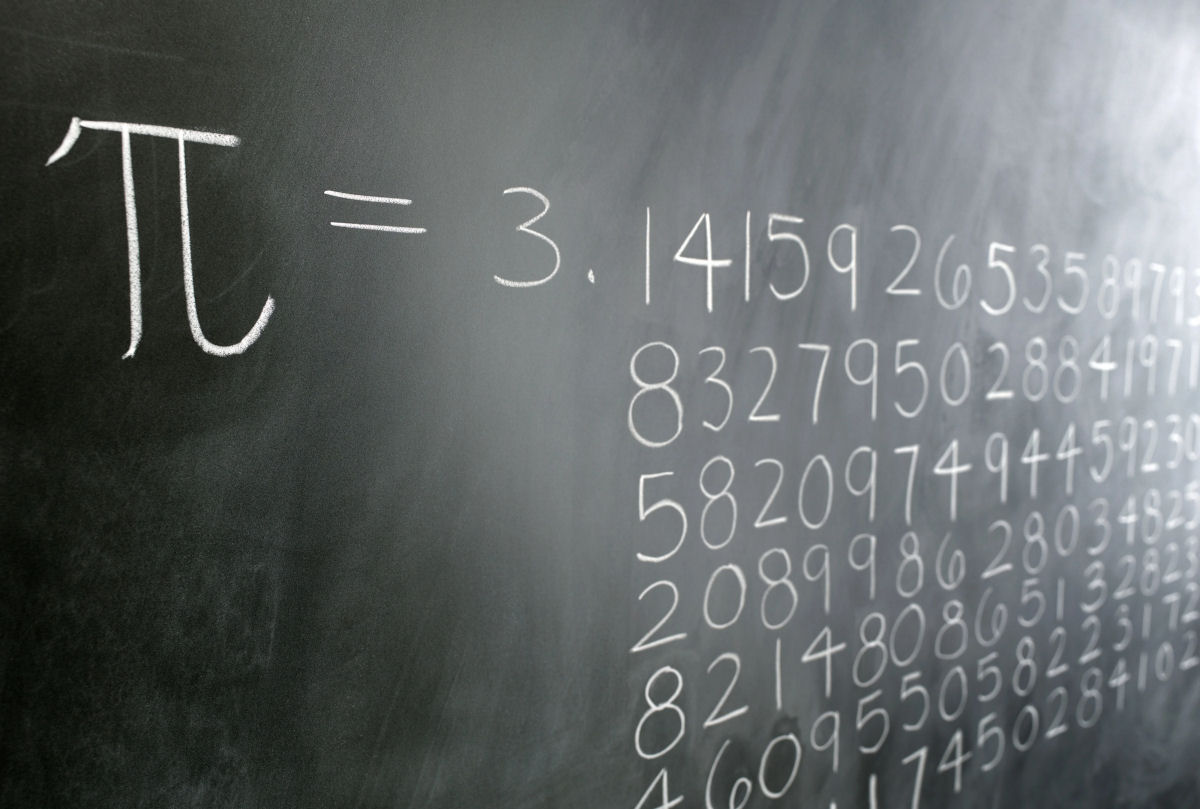
Os historiadores não sabem ao certo quando ou como esse número foi descoberto pela primeira vez, mas ele é conhecido de alguma forma há quase 4.000 anos.

O antigo matemático grego Arquimedes de Siracusa foi o primeiro a fornecer um cálculo rigoroso de o π, usando um método geométrico com polígonos.

Estimativas dele aparecem nos trabalhos de matemáticos gregos, babilônicos, chineses e indianos da antiguidade. E acredita-se até que tenha sido usado na construção das pirâmides egípcias.

Os matemáticos o estimavam inscrevendo polígonos em círculos. E por volta do ano 1400, ele já havia sido calculado com até dez casas decimais.

Mas o pi só se tornou π na década de 1700, primeiro por William Jones em 1706 e depois popularizado por Leonhard Euler em 1737.

Então, quando eles finalmente descobriram o valor exato em vez de apenas estimar? Na verdade, nunca!

Veja bem, a razão entre a circunferência de um círculo e seu diâmetro é o que se conhece como um número irracional, que nunca pode ser expresso como uma razão entre dois números inteiros.
Você pode chegar perto, mas não importa quão precisa seja a fração, ela sempre estará um pouquinho errada.

Então, para escrevê-la em sua forma decimal, você teria uma série contínua de dígitos começando com 3,14159 e continuando para sempre!

É por isso que, em vez de tentar escrever um número infinito de dígitos todas as vezes, simplesmente nos referimos a ele usando a letra grega π.

Hoje em dia, testamos a velocidade dos computadores fazendo-os calcular pi, e os computadores quânticos conseguiram calculá-lo até dois quatrilhões de dígitos.

As pessoas até competem para ver quantos dígitos conseguem memorizar e estabeleceram recordes por lembrar mais de 67.000 deles. Mas para a maioria dos usos científicos, você só precisa dos primeiros quarenta ou mais.

E quais são esses usos científicos? Bem, praticamente qualquer cálculo envolvendo círculos, desde o volume de uma lata de refrigerante até as órbitas de satélites. E não se trata apenas de círculos.

Como também é útil no estudo de curvas, π nos ajuda a entender sistemas periódicos ou oscilantes, como relógios, ondas eletromagnéticas e até música.

Em estatística, π é usado na equação para calcular a área sob uma curva de distribuição normal, o que é útil para descobrir distribuições de pontuações de testes padronizados, modelos financeiros ou margens de erro em resultados científicos.

Como se não bastasse, o π é usado em experimentos de física de partículas, como os que utilizam o Grande Colisor de Hádrons, não apenas devido ao seu formato redondo, mas de forma mais sutil, devido às órbitas em que partículas minúsculas se movem.

Cientistas até usaram o π para provar a noção ilusória de que a luz funciona tanto como partícula quanto como onda eletromagnética e, talvez o mais impressionante, para calcular a densidade de todo o nosso universo, que, aliás, ainda contém infinitamente menos elementos do que o número total de dígitos do π.